Critical
Authors: Benjamin Qi, Mihnea Brebenel, Kevin Sheng
Finding nodes that must be visited along any path.
Prerequisites
- Gold - Cycle Finding
Focus Problem – try your best to solve this problem before continuing!
| Resources | ||||
|---|---|---|---|---|
| Princeton | Made by the creator of the algorithm himself! | |||
| Wiki | Wiki Definition | |||
| Blog | ||||
| Blog | ||||
Initial Approach
These critical nodes that the problem talks about are commonly known as dominators. Let's define as the set of nodes that dominate node .
The dominator of the starting node is itself, and the set of dominators for any other node is the intersection of the set of dominators for all ancestors of node .
Implementation
The following code uses the above recurrence. However, it's too slow and uses too much memory. We'll try to optimize this moving on!
Time complexity: .
C++
#include <bitset>#include <iostream>#include <vector>using std::bitset;using std::cout;using std::endl;using std::vector;const int MAX_N = 1e5;
Optimizing With Trees
In this approach, we are going to build the dominator tree of the graph.
Before we discuss this though, let's set up some terms we're going to use throughout this module:
- A node strictly dominates another node if dominates and .
- Let the immediate dominator of , or , be the unique node such that it strictly dominates node and every other dominator of node strictly dominates node .
- Let the semi-dominator of , or , be a such that there's a path from to and for every intermediate node along the path from to , excluding the ends. If there's multiple nodes that satisfy this requirement, we take the node with the smallest .
- Let the relative dominator of , or , be the vertex on the path from to in the Euler tour tree with the lowest sdom node number. Unlike with the sdom, ties in this function can be broken arbitrarily.
A dominator tree is a tree where each node's children are those nodes it immediately dominates. The start node is the root of the tree.
Given this definition, we can see that if a node dominates another, then the former is an ancestor of the latter in the dominator tree. Thus, the answer to the CSES problem is the set of all nodes that lie on the path from the root to node in the tree.
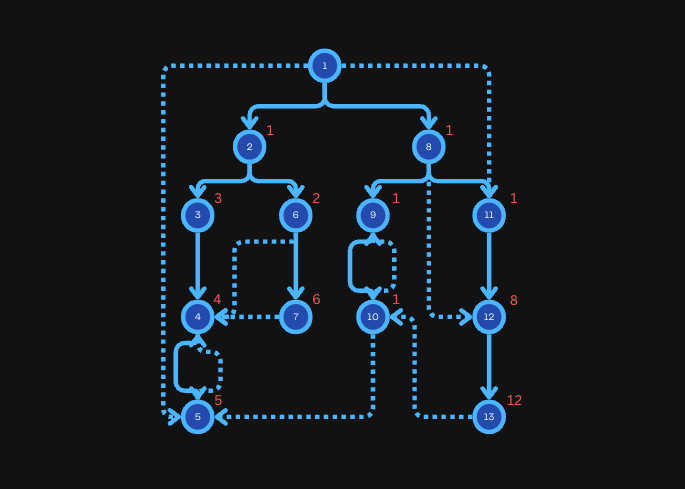
The following graph shows the sdom for every node. The full-color edges represent the edges part of the DFS tree.
Important properties
Proofs of these properties are located later in the module. For all of these properties, let be a node that isn't the starting node.
- is a proper ancestor of is the DFS tree.
- If , then .
- If not, then
Algorithm Overview
Before we get into the nitty-gritty, here's a brief outline of how exactly we're going to build up this dominator tree.
- Compute the sdom of every node besides the start.
- Compute the rdom of every node besides the start.
- Visit all the vertices in the DFS tree and calculate their immediate dominator using the second and third properties that were listed above. Notice that due to how we defined the rdom of a node, a preorder traversal will always visit the rdom of a node before the node itself if the two aren't the same.
The first and second steps are awfully vague- let's clear those up now, shall we?
Computing
We can compute as the minimum node in the intersection of the following groups:
- All the nodes such that there's an edge from to and .
- All the values of where is any node such that there's an edge from to and . To be more mathematically precise, we can define this group as
The proof of why this works is beyond the scope of this module.
Implementing
We first perform a preorder DFS traversal of the graph from the source node and keep track of all the entry times of the nodes.
Then, we compute the sdom for all nodes by applying the formula mentioned in the previous section. To do this, we iterate over the traversal in reverse order and maintain the nodes we've gone over in a DSU.
However, the DSU we use for this algorithm is going to be a little different.
We unite nodes as usual, but the find function differs.
Say is the root of the component we're calling find on.
The node we're calling find on happens to be x, then we return x as usual.
However, if it's some other node, then we return a node with the minimum sdom that lies on the path from to .
To process node we iterate over all nodes that have an edge directed towards it.
If comes before in the preorder traversal, then is an ancestor of and would not have been processed till now.
In that case, find(v) would return itself.
If not, then find(v) would return a node lying on the path from to the root in its DSU component with the smallest sdom.
If you're still a bit confused by this explanation, psuedocode for it is located on slide 33 of the Princeton slides given at the start of this module.
Computing
The rdom of a node is the node with the sdom that comes earliest in the traversal. Since this reduces to finding the minimum of a value along a certain path in a tree, we can implement this using an augmentation of binary jumping.
Implementation
Time Complexity:
C++
#include <algorithm>#include <cassert>#include <cmath>#include <cstdint>#include <functional>#include <iostream>#include <vector>using std::cout;using std::endl;
Cycles
Focus Problem – try your best to solve this problem before continuing!
Explanation
The problem asks as to find the an intersection node of all cycles, if it exists.
First, let's remove the nodes that don't belong to any cycle. To todo this, we can recursively remove the nodes without any outgoing edge. By "recursively," we mean that after finishing with a node we can check its parents to see if the parents have no outgoing edges as well.
Now our graph is basically a bunch of cycles. Assuming that the intersection of all cycles is not empty, we reduce the cycles node by node. The last node standing is be the intersection.
Implementation
Time Complexity:
C++
#include <functional>#include <iostream>#include <unordered_set>#include <vector>using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(NULL);
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| CF | Hard | ||||
| Kattis | Hard |
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!